My notes on a brilliant connectome paper

Here are my (short, first-draft full of mistakes) notes for the brilliant paper

“Closures and Cavities in the Human Connectome”

by Ann Sizemore, Chad Giusti, Richard F. Betzel, and Danielle S. Bassett.

Link

Does the brain contain arithmetic progressions?

(version 2, will try to expand)

Imagine that you have an alphabet consisting of some symbols . Now imagine another symbol; call it . Let us say that I know how to construct words; i.e., know how to construct sequences of letters, using only letters from the alphabet. Now a friend of mine can interrupt me at any point of the sequence by shouting . Suppose now that I only know the letters and each time I try to spell a 5-letter word using these letters a friend of mine interrupts me by shouting the letter . If she is really aggressive, the outcome could be something like . If not I could say something like . A word containing at least one interruption is called a root.
Now imagine that someone else listens to us. If I start saying the word ‘door’ and my friend interrupts me the listener can guess the following:

1. I said
2. I said
3. I said
4. I said

This set is called the combinatorial line of the root .
Making the previous a little bit more mathematical, let be a finite symbol alphabet. Let be the new symbol. Words are considered as sequences of symbols of the alphabets without containing the letter . Sequences containing at least one symbol are called roots. If in each such root we replace the with each symbol of the alphabet, we get a collection of words rooted by the specific root. A combinatorial line is the set of words that stems from simultaneous replacement each time of the symbol by one of the alphabet symbols.

Exercise: Suppose that there exists an alphabet consisting of 0 and 1. Calculate the number of combinatorial lines for sequences of length .
(Solution Here)

Brain parcellation
In order for neuroscientists to study the properties of each area in the brain (either neurophysiological or, if someone considers mathematical models of nodes and edges in the brain, topological properties), they use some specific parcellation where each area has specific coordinates in a standard space.

What I will do here is play a little bit with combinatorial lines and the extended-AAL atlas coordinates. These coordinates characterize a set of cortical and subcortical areas as well as areas of the cerebellum, commonly used in fMRI. In short, cortical ROIs are from the FSL Harvard-Oxford Atlas maximum likelihood cortical atlas, subcortical ROIs are from the FSL Harvard-Oxford Atlas maximum likelihood subcortical atlas, and cerebellar parcellation is from the AAL Atlas. Here, I used the labels and coordinates (excluding the final 8 “Vermis” areas) as found in the Conn toolbox (https://www.nitrc.org/projects/conn/).

Binary encoding and combinatorial lines
I will encode these areas based on a specific binary encoding. Therefore, in this case our alphabet consists of two symbols: or . They way to assign each area to the aforementioned encoding is completely arbitrary.
For example, I can have something like this:

; Hippocampus

 

; Posterior Cingulate

 

; …

 

 

 

 

 

The pair can be considered as a combinatorial line (with root ) whereas the pair cannot. Now, for every entry in the encoding, we are going to search all other entries and see if, as a pair, they become a combinatorial line.

What I did for this post is to encode the areas (121 in total) based on their Euclidean distance from a reference point. For each area, I calculated the Euclidean distance between its coordinates and the point. Then, I sorted them in an ascending order and used a 8 bit binary encoding. Therefore the will be the area with smallest distance from the will be the area with somewhat bigger distance and so on.
What I did afterwards was to find all the combinatorial lines in this encoding for each area. Remember that, since we are using binary encoding, a combinatorial line will be a pair of areas; for example, and could be the combinatorial line with root (there can be other roots for this pair). Eventually, for each area, I found all the combinatorial lines (pairs that include the respective area) that also belong to the encoding.

Results
Having all the combinatorial lines for each area, I tried to plot some of them! In the next pictures (you may need to click and zoom for a better resolution), I depict as the big yellow node the area that I considered. The other nodes stand for the areas that the combinatorial lines of the considered area consist of.

Here is the left angular gyrus.

Here is the right angular gyrus.

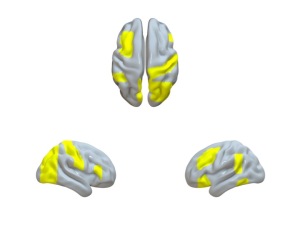
(I was hoping for a default-mode network but didn’t see a clear picture of it : )).

Discussion
What I described previously is an attempt to encode brain areas and find combinatorial lines within this encoding.

Combinatorial lines can be viewed as geometrical lines in a dimensional cube of words, where is the set of symbols for the alphabet. An interesting aspect is whether, given a specific alphabet and some categorization (in terms of each word belonging to a category), there exist combinatorial lines that are in the same category.

The Hales-Jewett theorem claims that there is a length of words (or dimension of the cube) such that every coloring on words induces a monochromatic combinatorial line.

Theorem (Hales-Jewett, 1963)

Given distinct colors and a finite alphabet of symbols, there is a dimension such that, for every coloring of the cube , there exists a monochromatic combinatorial line.

One can think of this as a game. If each color corresponds to a player’s move, there exists a dimension (that depends on the number of the symbols used in the game and the number of players) such that a player can obtain a multi-dimensional line of her own color (pretty much win).

My line of thought is the following:

In recent years, neuroimaging studies have adopted network models in order to analyze patterns of correlations between the neurophysiological signals of each brain area. For example, a standard methodology assumes that each area is a node in the network and edges between them exist if there is a significant correlation between the time course of their blood-oxygenated-dependent signals. Above and beyond this, one might explore the properties of each node in the network using standard network techniques.
Now, suppose that colors correspond to properties of the network. For example, each node (word) in the cube is assigned to a color based on some specific topological property (for example the number of shortest paths in the network that pass through it).

Question: If we know that, given a specific number of colors and symbols, there exists a dimension that induces monochromatic combinatorial lines, can these lines correspond to areas of the brain that share these properties by using  “suitable” color definitions and encoding each area?

In other words, can the fact that some brain areas share similar topological properties be interpreted in terms of the existence of monochromatic combinatorial lines in a suitable brain area encoding (for example encoding based on their distance from a reference point like before or their neurotransmitters density and regarding specific topological properties)?

One can go beyond this and, using the Hales-Jewett theorem, can argue that the existence of monochromatic combinatorial lines in a set imply arithmetic progressions of specific length.

The following theorem exists regarding the existence of monochromatic arithmetic progressions and can be proved using the Hales-Jewett theorem.

Theorem (Van der Waerden, 1927)
Given distinct colors and , there exists a such that for every coloring coloring of the set , there exists at least one monochromatic arithmetic progression of terms:
.

I would love to argue that areas that share the same properties can be viewed as parts of monochromatic arithmetic progressions.

General methodological question: Is there any connection between the topology of brain networks and combinatorial theories that argue about whether the size of the structure implies a specific property?

That’s all for now but I will try to expand more in later posts.

FCRC talks

Mental Wilderness

I was at FCRC (the CS conference conglomerate that happens once every 4 years), June 13-19. Here are some of the talks I found particularly memorable.

Personal notes on FCRC talks are at https://workflowy.com/s/wkI79JfN0N and on STOC/CCC/EC talks (very rough) are at https://dl.dropboxusercontent.com/u/27883775/wiki/math/pdfs/stoc.pdf. Note that neither has been edited.

FCRC award/plenary talks

• Turing award lecture (The Land sharks are on the squawk box), Michael Stonebraker (https://www.youtube.com/watch?v=BbGeKi6T6QI): Stonebraker draws parallels between his work in building Postgres, a relational database system, and his cross-country bike trip. He described numerous challenges and how they were overcome in both situations, concluding that they were both about “making it happen”.
• Interdisciplinary research from the view of theory, Andrew Yao: Yao comes from the viewpoint of theoretical computer science but has then worked on connections to physics (quantum computation), economics (auction theory), and cryptography (certifiable randomness). Theoretical computer science started with computability…

View original post 1,006 more words

Paper of the day 03/31/15

Paper of the day:

Representations of real numbers as sums and products Liouville Numbers

by P . Erdős

Monte Carlo Methods

https://www.cs.cmu.edu/~ggordon/MCMC/ggordon.MCMC-tutorial.pdf

Paul Erdös’s 102-ennial

in theory

Paul Erdös would be 102 year old this year, and in celebration of this the Notices of the AMS have published a two-part series of essays on his life and his work: [part 1] and [part 2].

Of particular interest to me is the story of the problem of finding large gaps between primes; recently Maynard, Ford, Green, Konyagin, and Tao solved an Erdös $10,000 question in this direction. It is probably the Erdös open question with the highest associated reward ever solved (I don’t know where to look up this information — for comparison, Szemeredi’s theorem was a $1,000 question), and it is certainly the question whose statement involves the most occurrences of “$latex log$”.

View original post

Deep learning for chess

Very interesting post on how to construct a simple neural network for chess AI.

http://erikbern.com/?p=841

SUIF publications

Papers from the Stanford Compiler Group

http://suif.stanford.edu/papers

The Krein-Milman Theorem

Nirakar Neo's Blog

1. The Krein-Milman theorem in Locally Convex Spaces

My project work this semester focuses to understand the paper the Krein-Milman Theorem in Operator Convexity by Corran Webster and Soren Winkler, which appeared in the Transactions of the AMS [Vol 351, #1, Jan 99, 307-322]. But before reading the paper, it is imperative to understand the (usual) Krein-Milman theorem which is proved in the context of locally convex spaces. My understanding of this part follows the book A Course in Functional Analysis by J B Conway. To begin with we shall collect the preliminaries that we shall need to understand the Krein-Milman theorem.

1.1. Convexity

Let $latex {mathbb{K}}&fg=000000$ denote the real($latex {mathbb{R}}&fg=000000$) or the complex($latex {mathbb{C}}&fg=000000$) number fields. Let $latex {X}&fg=000000$ be a vector space over $latex {mathbb{K}}&fg=000000$. A subset of a vector space is called convex if for any two points in the subset, the line segment joining them…

View original post 3,073 more words

Actions do change the world.

Quantum Frontiers

I heard it in a college lecture about Haskell.

Haskell is a programming language akin to Latin: Learning either language expands your vocabulary and technical skills. But programmers use Haskell as often as slam poets compose dactylic hexameter.^*

My professor could have understudied for the archetypal wise man: He had snowy hair, a beard, and glasses that begged to be called “spectacles.” Pointing at the code he’d projected onto a screen, he was lecturing about input/output, or I/O. The user inputs a request, and the program outputs a response.

That autumn was consuming me. Computer-science and physics courses had filled my plate. Atop the plate, I had thunked the soup tureen known as “XKCD Comes to Dartmouth”: I was coordinating a visit by Randall Munroe, creator of the science webcomic xkcd, to my college. The visit was to include a cake shaped like the Internet, a robotic velociraptor, and

View original post 249 more words